부동소수점의 메모리 저장방식 ( IEEE 754)
부동소수점 (Floating Point) 이란?
비트는 모든 데이터를 0과 1로만 저장할 수 있다. 그런데 3.14나 -2.5 같은 실수는 어떤식으로 저장하는걸까?
이를테면 아래의 식에서 좌변은 우변과 같다는 것을 알 수 있는데
- 1234000 = 1.234 × 10³
- 0.000567 = 5.67 × 10⁻⁴
컴퓨터에서는 2진수를 사용하므로 아래와 같이 변환 가능함
- 6.25 = 1.1001 × 2²
즉 유효숫자 × 2^지수 형태로 저장하는 것을 부동소수점이라 한다.
IEEE 754
전 세계 컴퓨터가 같은 방식으로 실수를 저장하기 위한 국제 표준.
단정밀도 Single Precision (float, 32비트)
[부호 1비트] [지수 8비트] [가수 23비트]배정밀도 Double Precision (double, 64비트) (단정밀의 두배라서 배정밀도 라고 하는듯)
[부호 1비트] [지수 11비트] [가수 52비트]즉 실수를 2진수 변환, 정규화, IEEE 754 규약에 맞춰 변환하는 단계를 거친다.
여기서 정규화란?
같은 숫자를 다음과 같이 여러 방식으로 표현할 수 있다.
- 123.45 = 1.2345 × 10²
- 123.45 = 12.345 × 10¹
- 123.45 = 123.45 × 10⁰
컴퓨터도 마찬가지로 2진수에서 이렇게 되는데.
- 11.011₂ = 1.1011 × 2¹
- 11.011₂ = 110.11 × 2⁻¹
정규화는 항상 같은 형태로 통일하는 것을 말한다.
IEEE 754 정규화 규칙은 소수점 앞에 항상 1이 오도록 만드는 것
11.011₂ → 1.1011 × 2¹ (정규화됨 ✓)
110.11₂ → 1.1011 × 2² (정규화됨 ✓)
0.1101₂ → 1.101 × 2⁻¹ (정규화됨 ✓)정규화의 장점
- 저장공간 절약: 맨 앞의 1은 항상 있으므로 저장하지 않음
- 표현 통일: 같은 숫자를 항상 같은 방식으로 저장
- 정밀도 향상: 더 많은 유효숫자 저장 가능
예제1)
float debuffSpeed = -3.375f
1단계: 2진수 변환
정수 부분 (3):
- 3 ÷ 2 = 1 나머지 1
- 1 ÷ 2 = 0 나머지 1
- 결과: 11₂
소수 부분 (0.375):
- 0.375 × 2 = 0.75 → 0
- 0.75 × 2 = 1.5 → 1
- 0.5 × 2 = 1.0 → 1
- 결과: 0.011₂
합치면: 3.375₁₀ = 11.011₂
2단계: 정규화
11.011₂ = 1.1011 × 2¹
3단계: IEEE 754 Single Precision 변환
부호 비트: 음수이므로 1
지수 비트:
- 실제 지수: 1
바이어스(지수를 양수로 만들어 저장 간편화): 127 (Single Precision)
- 저장값: 1 + 127 = 128
- 128₁₀ = 10000000₂
가수 비트:
- 1.1011에서 소수점 이후: 1011
- 23비트로 확장: 10110000000000000000000
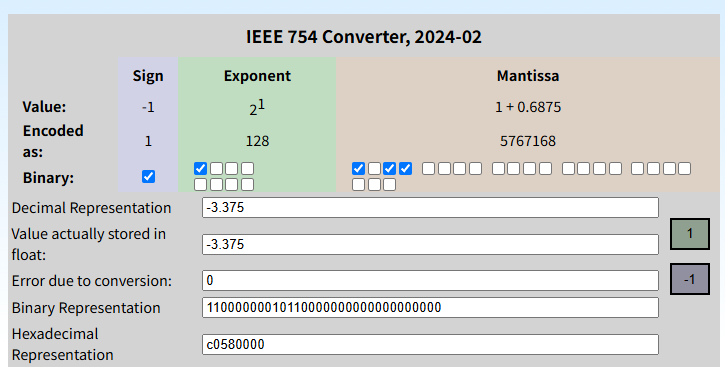
결과 확인
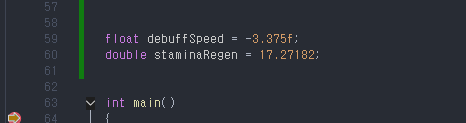
브레이크 포인트를 잡아놓고 디버깅하면
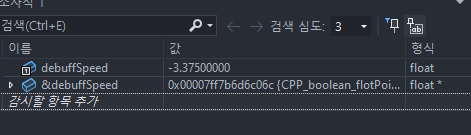
이렇게 변수 debuffSpeed의 메모리 주소가 0x00007FF7A4AEC06C 으로 나오는데
메모리에 해당 주소를 찾아보면
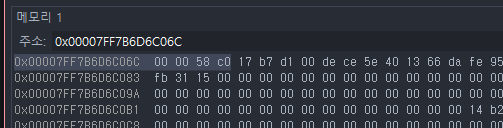
이렇게 리틀엔디안으로 저장되어 있는 0xC0580000 을 확인할 수 있다. 16진수 C0580000을 확인해보면
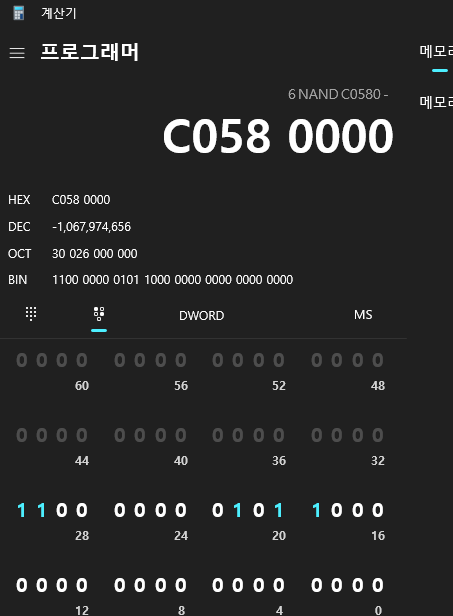
부호 1 (1비트 음수)
지수 1000 0000 (8비트)
가수 10110000000000000000000 (23비트) 를 확인할 수 있다!
예제2)
double staminaRegen = 17.27182
1단계: 2진수 변환
정수 부분 (17):
- 17 ÷ 2 = 8 나머지 1
- 8 ÷ 2 = 4 나머지 0
- 4 ÷ 2 = 2 나머지 0
- 2 ÷ 2 = 1 나머지 0
- 1 ÷ 2 = 0 나머지 1
- 결과: 10001₂
소수 부분 (0.27182):
- 0.27182 × 2 = 0.54364 → 0
- 0.54364 × 2 = 1.08728 → 1
- 0.08728 × 2 = 0.17456 → 0
- 0.17456 × 2 = 0.34912 → 0
- 0.34912 × 2 = 0.69824 → 0
- 0.69824 × 2 = 1.39648 → 1
- 0.39648 × 2 = 0.79296 → 0
- 0.79296 × 2 = 1.58592 → 1
- ... (계속)
- 결과: 0.01000101...₂ (근사값)
합치면: 17.27182₁₀ ≈ 10001.01000101...₂
2단계: 정규화
10001.01000101...₂ = 1.000101000101... × 2⁴
3단계: IEEE 754 Double Precision 변환
부호 비트: 양수이므로 0
지수 비트:
- 실제 지수: 4
- 바이어스: 1023 (Double Precision)
- 저장값: 4 + 1023 = 1027
- 1027₁₀ = 10000000011₂
가수 비트:
- 1.000101000101...에서 소수점 이후: 000101000101...
- 52비트로 확장
결과 확인
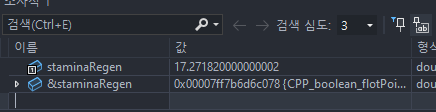
같은 방식으로 해당 변수의 메모리 주소를 확인하고 저장된 데이터를 보면
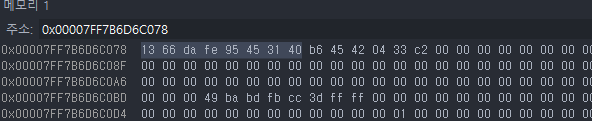
잘 저장되어 있다. 계산기 켜서 확인하면 아래와 같다.

부호 0
지수 10000000011
가수 0001010001011001010111101111110110100110011000010011..
정밀도의 차이
- float (32비트): 약 7자리 정밀도
- double (64비트): 약 15-16자리 정밀도
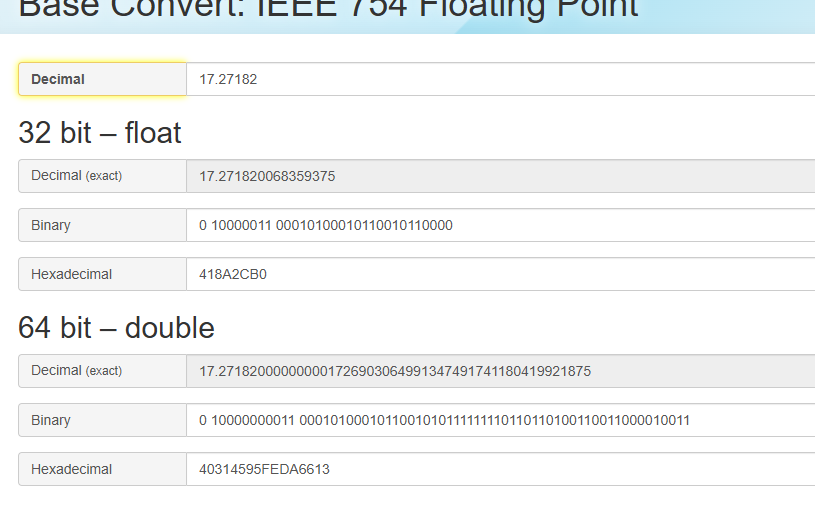
예제2에서 확인했던 17.27182를 보면 flaot와 double을 사용했을 때 정밀도가 다른것을 확인할 수 있다. (사진상 10진수정밀도 부분)
따라서 더 정확한 계산이 필요할 때는 double을 사용해야함
또한 부동소수점은 확인한 바와 같이 근사값으로 저장되기 때문에 근사값 + 근사값이 더해짐을 인지해야한다.
float a = 0.1f + 0.2f;
// a는 정확히 0.3이 아닐 수 있음